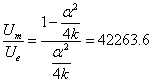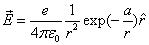
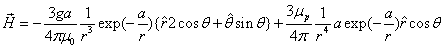
Let us assume that the following is the proton electromagnetic structure:
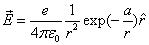
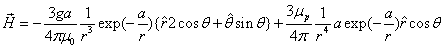
Proton Electric charge
The proton electric charge density distribution is given as:
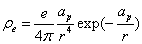
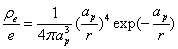
X coordinate is the radius with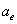 
as the distance unit
Y coordinate is the electric charge density with e as the electric charge unit.
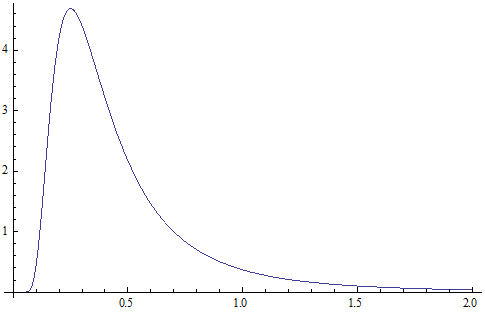
Proton electric charge of radius r sphere distribution
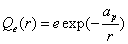
Proton Magnetic Charge
Since we know the magnetic charge density is:
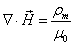
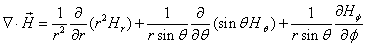
Then the electron magnetic charge becomes
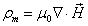
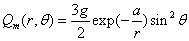
When
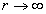and 
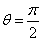
We get the electron magnetic charge of the northern hemisphere as the following:
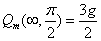
When
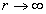and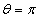 
Then
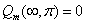
The proton as a whole has zero magnetic charge
The proton's electromagnetic field angular momentum
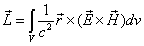
The proton electromagnetic field equation is given as:
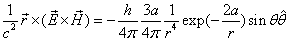
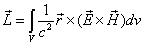
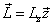
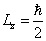
Based on the proton electromagnetic model, the proton always has half spin, the proton spin has electromagnetic origin.
Proton's magnetic moment
The proton magnetic moment is shown below
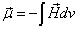
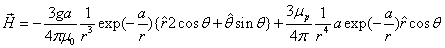
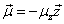
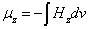
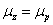
Proton's Electric field energy
The electric field energy density is as the following:
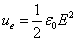
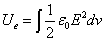
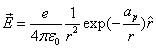
The total electric energy of sphere of radius r
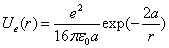
When
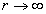
We can get the proton's total electric field energy as
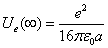
Proton's magnetic field energy
The magnetic field energy density is:
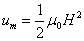
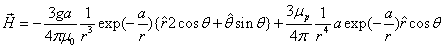
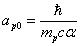
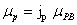
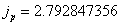
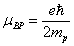
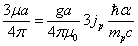
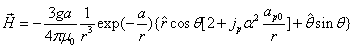
The proton's magnetic field energy then becomes
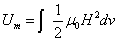
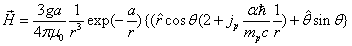
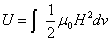
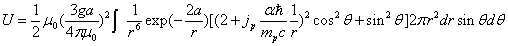
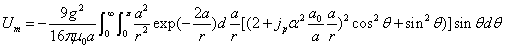
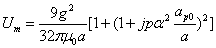
If the proton's electric field energy is
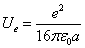
Then we get the proton's electromagnetic field energy as the following
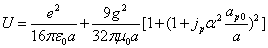
Let us define
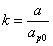
By substituting k into the above formula, we have
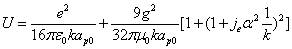
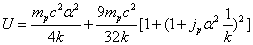
Assuming the proton mass has an electromagnetic origin, then we have
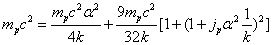
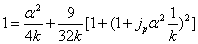
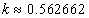
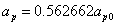
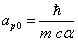
For the proton, the ratio of the magnetic energy to the electric field energy is:
