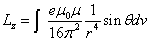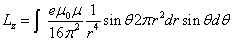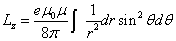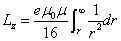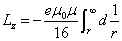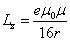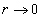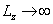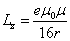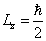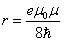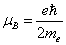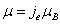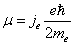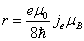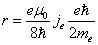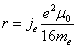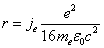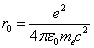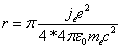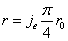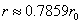The electron has four basic parameters, which are: one unit negative electric charge -e, half spin 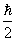 , electron self energy
, electron self energy 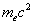 , and also electron magnetic moment
, and also electron magnetic moment 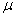 .
.
The simplest electromagnetic model of the electron is shown below:
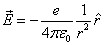
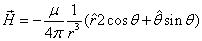
Where the electron's electric field is the point charge field, the electron's magnetic field is the magnetic dipole field, 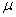 is the electron magnetic moment.
is the electron magnetic moment.
Based on the above two equation, we can see that the electric field has a spherical distribution, but the magnetic field does not have a spherical distribution.
In this model when 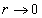 , both electric field strength and magnetic field strength become infinity, at the point
, both electric field strength and magnetic field strength become infinity, at the point 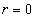 , it has the singularity problem.
Electron's electric point charge field
As we know, the electron has one unit electric charge and its own intrinsic electric field. The simplest model for the electron's electric field is the point charge model; electric charge only at the electron center
, it has the singularity problem.
Electron's electric point charge field
As we know, the electron has one unit electric charge and its own intrinsic electric field. The simplest model for the electron's electric field is the point charge model; electric charge only at the electron center 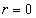 .
.
Based on the point charge model, the electron's electric field equation is shown below:
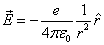
Where 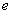 is the electric charge unit.
As we can see in the above equation, the electric field strength E becomes infinity when
is the electric charge unit.
As we can see in the above equation, the electric field strength E becomes infinity when 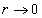 , electric field has a singularity when
, electric field has a singularity when 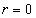 .
We can find out that the electric field in the electron's point charge model has a spherical symmetry. The electric energy density is:
.
We can find out that the electric field in the electron's point charge model has a spherical symmetry. The electric energy density is:
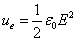
Thus we can get the electron's electric field energy density as follows:
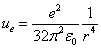
Let us calculate the electric field energy outside the sphere of radius r, which is:
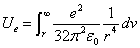
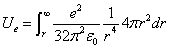
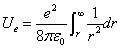
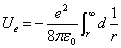
Thus, outside the sphere of radius r, the total electric energy is:
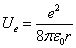
When
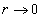
Then
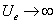
From the above the electron's total electric field energy based on the point charge model becomes infinity.
Electron's magnetic dipole field
The electron has the magnetic dipole moment, the electron act like a small magnet; the simplest model for the electron's magnetic field is the magnetic dipole field model
For the magnetic dipole field, the equation is as follows:
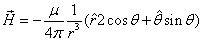
Where 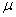 is the electron magnetic moment,
is the electron magnetic moment, 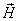 is the electron's magnetic field strength.
Based on the above equation, when
is the electron's magnetic field strength.
Based on the above equation, when 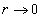 , the magnetic field strength becomes infinity, the point
, the magnetic field strength becomes infinity, the point 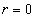 has magnetic singularity.
The divergence of magnetic field in spherical reference is as follows:
has magnetic singularity.
The divergence of magnetic field in spherical reference is as follows:
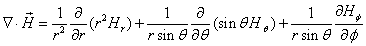
Where
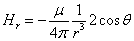
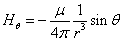
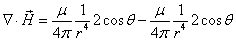
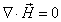
Thus we can see that the magnetic charge density is always kept at zero; so the total magnetic charge of the electron is also zero based on the magnetic dipole field model.
As we know, the magnetic field energy density is:
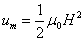
The magnetic field energy base on the magnetic dipole field model is:
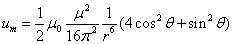
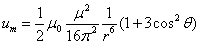
Let us calculate the electron's magnetic field energy outside the sphere of radius r, which is as follows:
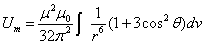
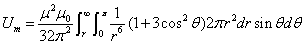
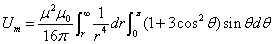
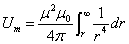
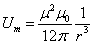
This is the electron's magnetic energy outside the sphere of radius r.
Thus, when
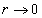
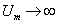
The total magnetic field energy becoming infinity is based on the magnetic dipole field model.
Similar to the electron's point charge model, the magnetic dipole model of the electron's magnetic fields also has the singularity problem.
The electron's electromagnetic field energy
The electron's electric field energy outside sphere of radius r based on the point charge model is as follows:
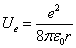
The electron's magnetic field energy outside sphere of radius r based on the dipole field model is:
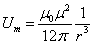
So the electromagnetic field energy outside sphere of radius r is as follows:
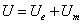
Where:
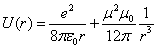
From the above, when
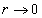
, then the total electromagnetic field energy of the electron becomes infinity.
Let us calculate the radius
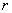
in which the electromagnetic field energy equates to electron's self energy
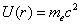
Thus
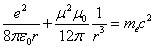
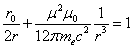
Where
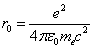
is the electron's classical radius.
The electron magnetic moment is as follows:
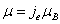
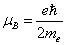
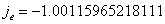
Thus
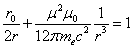
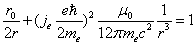
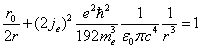
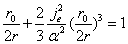
We can get the solution as:
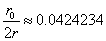
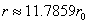
This is the radius value in which the electromagnetic field energy outside of sphere of radius r is equal to electron's self energy.
The electron's electromagnetic field angular momentum
The electron not only has self-energy, it also has electron spin, which is the electron intrinsic angular momentum. What is the origin of the electron spin? As the electromagnetic field can carry angular momentum, is it possible that the electron's electromagnetic field carry angular momentum? Furthermore, is it possible that the electron spin has an electromagnetic origin?
The electromagnetic field angular momentum density is defined as:
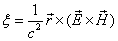
Based on the point model of electron's electromagnetic field:
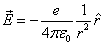
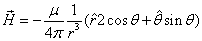
Let us calculate its electromagnetic angular momentum density:
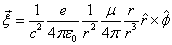
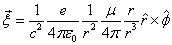
Thus
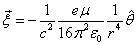
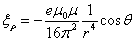
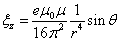
Due to the symmetry of the 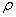 direction, the total
direction, the total 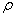 direction component of angular momentum becomes zero.
The z component of angular momentum is as follows:
direction component of angular momentum becomes zero.
The z component of angular momentum is as follows:
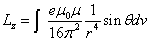
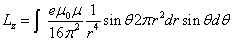
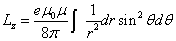
The total angular momentum outside the sphere of radius r is as follows:
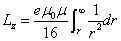
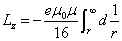
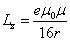
When
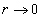
Then
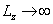
The angular momentum of the electron's electromagnetic field becomes infinity.
Let us calculate the radius r in which the outside sphere of radius r, the electromagnetic field angular momentum equals to electron spin value, which is:
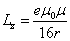
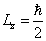
Then we have
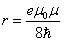
We know the Bohr magnetic moment is:
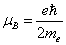
And the electron magnetic moment value is:
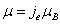
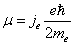
Then
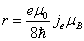
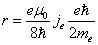
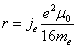
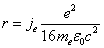
Furthermore, the classical electron radius is:
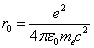
Thus
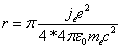
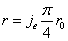
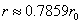
This is the radius in which the electromagnetic field angular momentum outside the sphere of radius r is equal to electron spin.
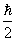 , electron self energy
, electron self energy 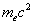 , and also electron magnetic moment
, and also electron magnetic moment 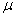 .
.
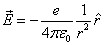
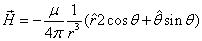
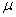 is the electron magnetic moment.
is the electron magnetic moment.
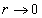 , both electric field strength and magnetic field strength become infinity, at the point
, both electric field strength and magnetic field strength become infinity, at the point 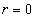 , it has the singularity problem.
Electron's electric point charge field
As we know, the electron has one unit electric charge and its own intrinsic electric field. The simplest model for the electron's electric field is the point charge model; electric charge only at the electron center
, it has the singularity problem.
Electron's electric point charge field
As we know, the electron has one unit electric charge and its own intrinsic electric field. The simplest model for the electron's electric field is the point charge model; electric charge only at the electron center 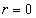 .
. 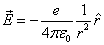
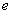 is the electric charge unit.
As we can see in the above equation, the electric field strength E becomes infinity when
is the electric charge unit.
As we can see in the above equation, the electric field strength E becomes infinity when 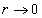 , electric field has a singularity when
, electric field has a singularity when 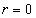 .
We can find out that the electric field in the electron's point charge model has a spherical symmetry. The electric energy density is:
.
We can find out that the electric field in the electron's point charge model has a spherical symmetry. The electric energy density is:
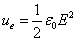
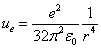
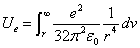
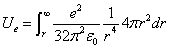
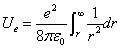
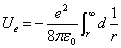
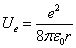
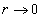
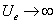
 is the electron magnetic moment,
is the electron magnetic moment, 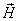 is the electron's magnetic field strength.
Based on the above equation, when
is the electron's magnetic field strength.
Based on the above equation, when 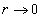 , the magnetic field strength becomes infinity, the point
, the magnetic field strength becomes infinity, the point 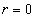 has magnetic singularity.
The divergence of magnetic field in spherical reference is as follows:
has magnetic singularity.
The divergence of magnetic field in spherical reference is as follows:
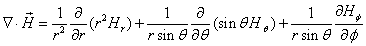
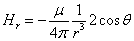
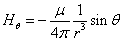
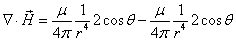
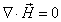
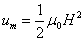
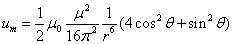
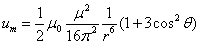
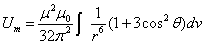
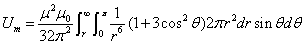
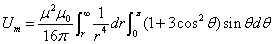
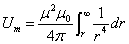
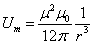
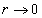
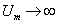
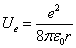
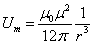
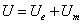
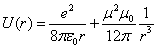
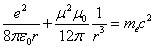
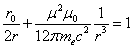
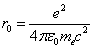
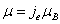
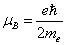
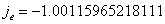
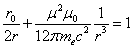
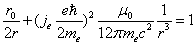
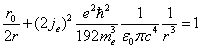
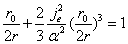
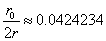
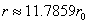
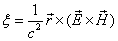
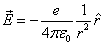
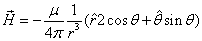
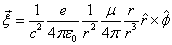
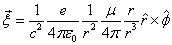
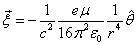
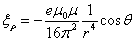
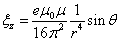
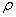 direction, the total
direction, the total 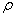 direction component of angular momentum becomes zero.
The z component of angular momentum is as follows:
direction component of angular momentum becomes zero.
The z component of angular momentum is as follows: