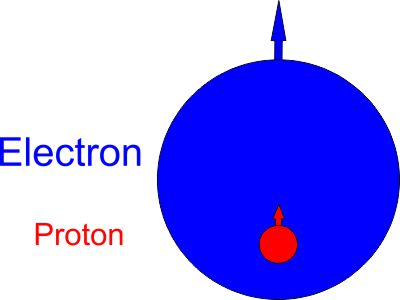
The hydrogen atom has only one proton and one electron. Below is the model of the hydrogen atom:
The spin direction is indicated by the direction of the arrow. The electron and proton have the same spin direction. The distance of the electron and proton, from the center of the electron to the center of the proton, is 2d. Often written as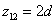 
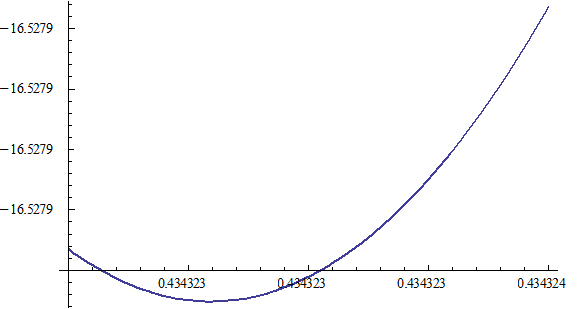
Let 1 represent electron, 2 represent proton. Then we have the electron electric field equation as:
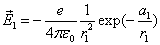
If
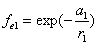
Then
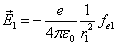
Given that the proton electric field is:
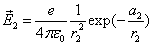
If
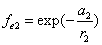
Then
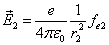
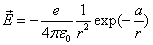
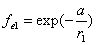
Thus the Hydrogen atom electric field is as the following:
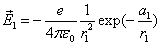
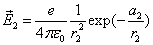
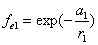
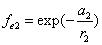
We know that the electric field energy density is:
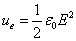
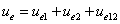
Where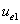 
is the first electron's electric field energy density, which is:
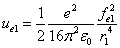
And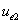 
is the proton's electric field energy density, which is:
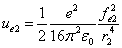
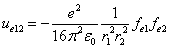
From the above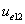 
is the Hydrogen atom's electric field binding energy density.
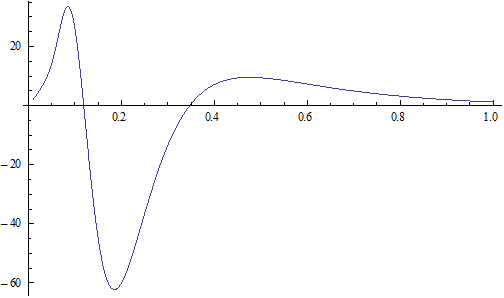
We can get the Hydrogen atom's electric binding energy as the following:
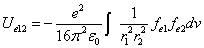
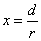
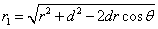
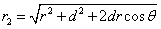
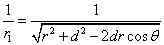
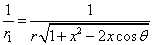
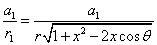
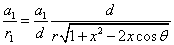
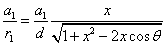
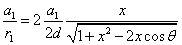
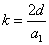
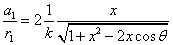
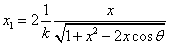
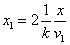
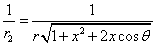
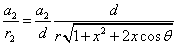
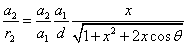
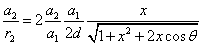
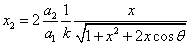
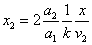
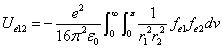
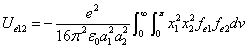
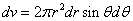
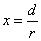
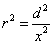
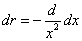
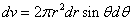
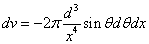
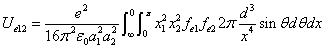
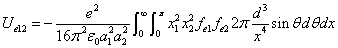
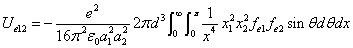
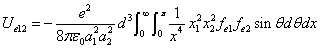
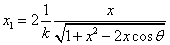
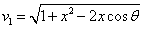
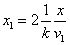
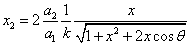
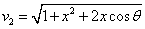
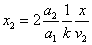
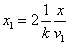
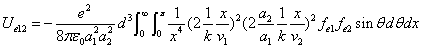
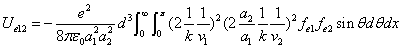
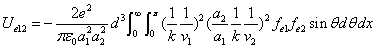
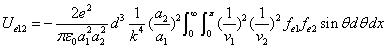
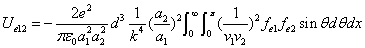
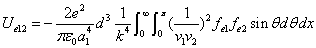
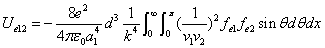
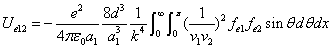
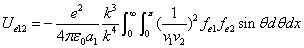
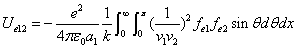
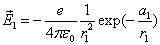
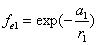
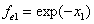
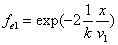
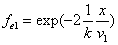
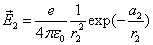
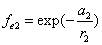
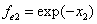
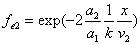
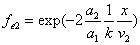
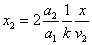
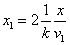
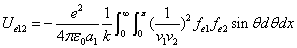
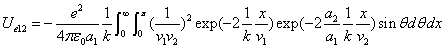
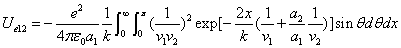
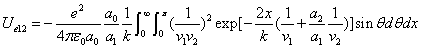
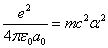
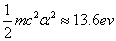
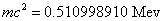
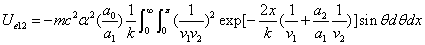
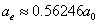
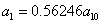
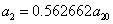
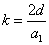
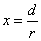
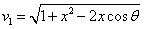
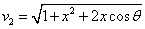
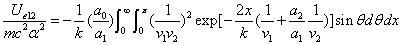
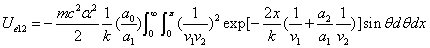
X coordinate is the distance between the proton and the electron with a0 as the unit
Y coordinate is the electron proton binding energy with ev as the unit
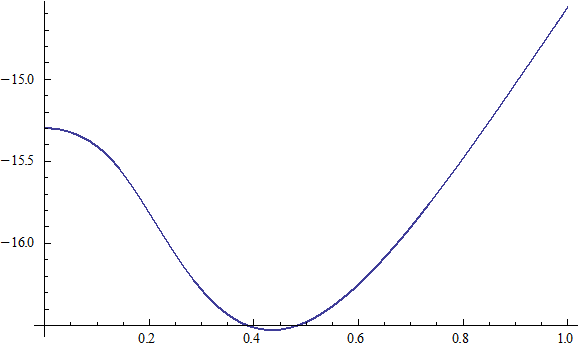
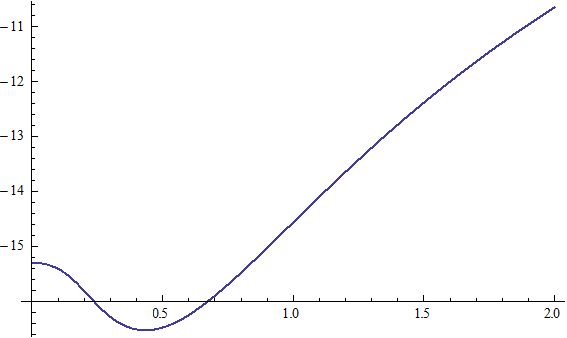
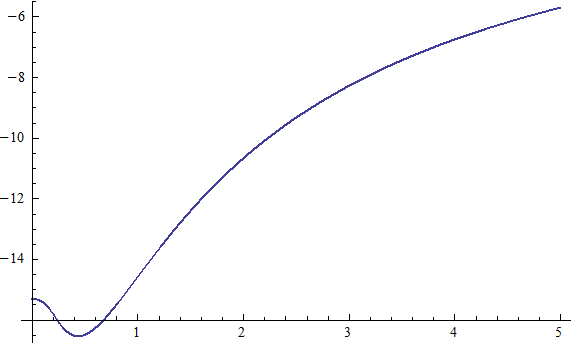
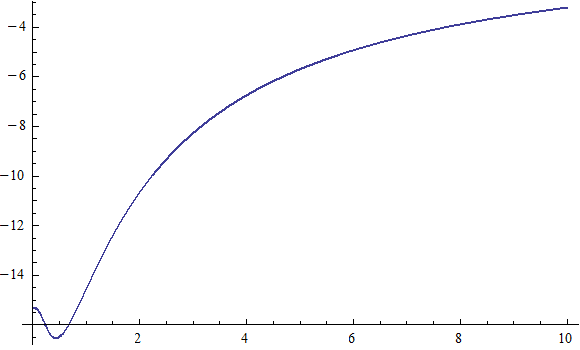
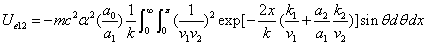
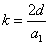
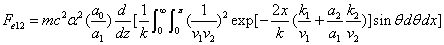
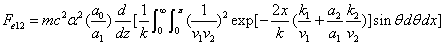
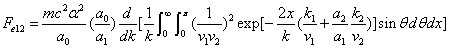
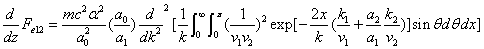
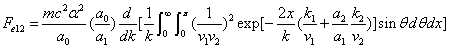
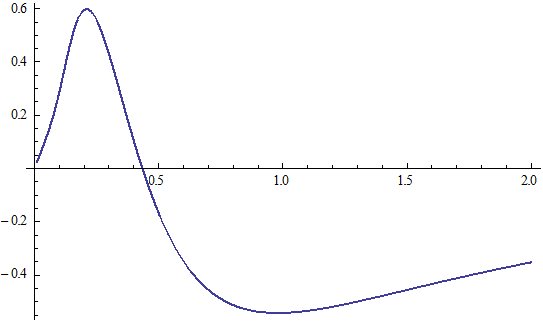
X coordinate is the distance between proton and electron with a0 as the unit
Y coordinate is the electron proton force with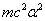 
/ a0 as the force unit
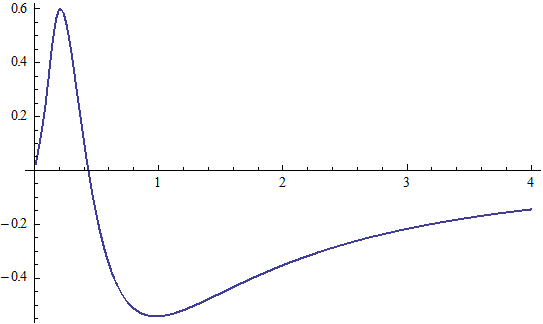
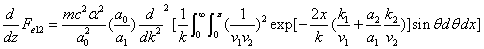
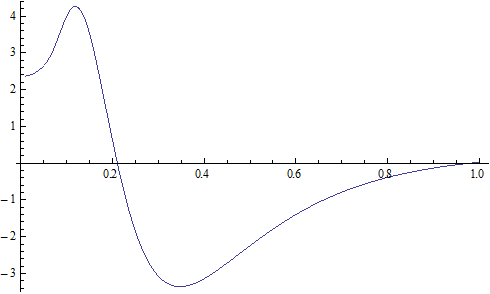
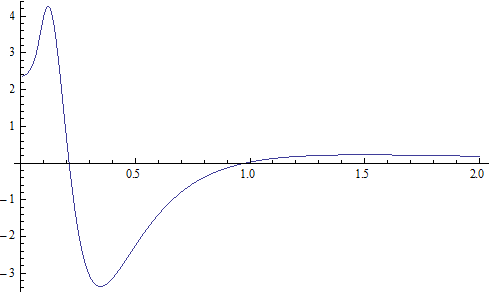
X coordinate is the distance between proton and electron with a0 as the unit
Y coordinate is the electron proton force differential with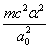 
as the unit
X coordinate is the distance between proton and electron with a0 as the unit
Y coordinate is the electron proton force 2nd differential with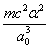 
as the unit
Hydrogen has only one proton and electron therefore in our hydrogen atom model, it does not get any extra energy. This is most likely to correspond to the near absolute zero temperature state such as solid or liquid state.
When
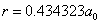
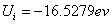
When hydrogen is heated in its solid or liquid state, it will emit light with all kinds of wavelengths, which corresponds to the hydrogen continuum spectrum.
When the hydrogen is in the thin gas state, and it absorbs enough extra energy with a flame or electric arc, the hydrogen will emit discrete spectrum called the hydrogen atom spectrum. Its ionization energy is
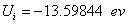
Let us assume that when the hydrogen atom emits discrete spectrum, the electron proton form a one-dimensional harmonic oscillator. The electron simple harmonic movement is as follows:
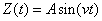
Electron proton within the hydrogen atom act like a simple LC circuit:
We represent
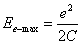as the maximum electric energy
We represent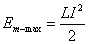 
as the maximum magnetic energy
Current as we know is
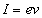
Where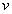
is the electron vibration frequency.
Then the total electromagnetic resonance energy will be as the following
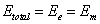
Thus we have
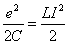
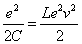
Thus we got the electron resonance frequency as
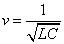
Since we know the characteristic impedance of electron as:
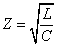
Then let us assume that the electron characteristic impedance is as follows:
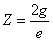
In which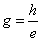 
Thus
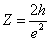
Then we have
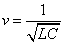
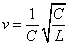
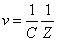
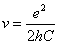
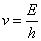
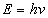
Thus we find out that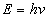 
is the result of electron electromagnetic resonance with the characteristic impedance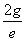 
With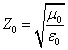 
as the impedance of free space
The EM wave velocity within free space is light speed.
For the instance with EM characteristic impedance Z, their EM wave velocity V will be
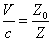
The EM wave velocity is inversely proportional to the EM wave impedance.
Thus EM wave velocity inside the hydrogen becomes
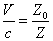
In which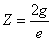 
Thus
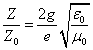
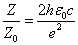
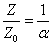
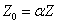
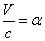
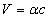
From the above, within the hydrogen atom, the EM velocity is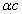 
Additionally, for the static electron, there is no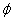 
direction magnetic field, therefore the static electron EM equation becomes:
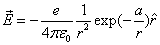
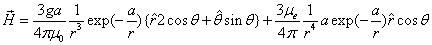
By assuming that when the electron makes a simple harmonic movement inside the hydrogen atom, the electron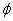 
direction magnetic field is:
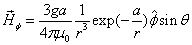
Then we have the electron electromagnetic moment as follows
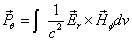
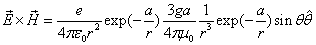
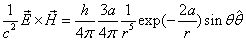
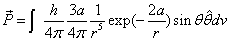
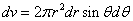
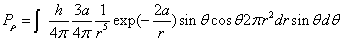
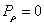
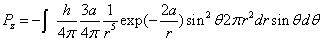
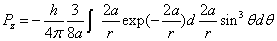
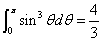
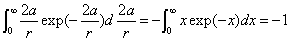
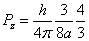
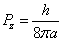
We know the electron electromagnetic field energy as
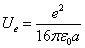
And we know,
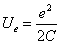
Equating both equations we get the electron capacitor C as
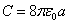
For the electron harmonic oscillator, we have
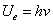
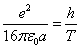
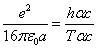
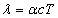
Where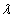 
is the EM wave length, 
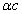is the EM wave velocity, 
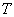is the EM wave period,
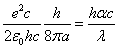
Given that
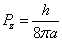
After substitution we have
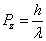
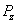is the electron electromagnetic moment,
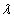is the electron electromagnetic resonance wavelength.
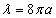
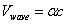
Thus we can get the electron resonance vibration moving equation as the following:
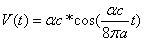
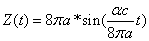
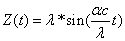
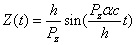
For the hydrogen atom, when it is in the thin gas state, and in the environment of flame or electric arc, it will emit a series of concrete spectrum. Its first spectrum series, the Lyman series is given as
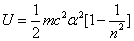
Where m is the reduced mass of electron and proton
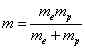
As we know the electron's electric energy
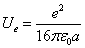
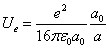
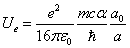
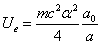
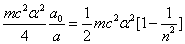
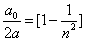
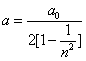
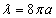
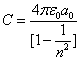
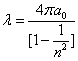
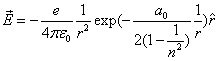
When
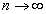
The ionization energy of the electron escaping from the hydrogen atom can be calculated as:
In the Ionization process, the electron ionization capacitor is:
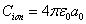
The hydrogen atom ionization energy can be rewritten as:
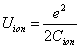
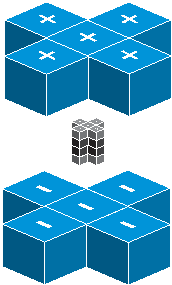
For the Z element, the atom has Z electron, according to their ionization energy from large to small, we can number these electron as K electron. When K=1, it relates to the largest ionization energy electron, when K=Z, it relates to the smallest ionization energy electron. Let us take for example, the atomic structure diagram of the element Neon:
Ne-10 electron configuration
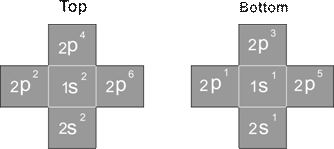
Element 1-10 Ionization energy table (ev as energy unit)
|
1s1 |
1s2 |
2s1 |
2s2 |
2p1 |
2p2 |
2p3 |
2p4 |
2p5 |
2p6 |
|
Z |
K |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
H |
13.6 |
|
|
|
|
|
|
|
|
|
2 |
He |
54.42 |
24.59 |
|
|
|
|
|
|
|
|
3 |
Li |
122.45 |
75.64 |
5.39 |
|
|
|
|
|
|
|
4 |
Be |
217.72 |
153.9 |
18.21 |
9.32 |
|
|
|
|
|
|
5 |
B |
340.23 |
259.38 |
37.93 |
25.15 |
8.3 |
|
|
|
|
|
6 |
C |
489.99 |
392.09 |
64.49 |
47.89 |
24.38 |
11.26 |
|
|
|
|
7 |
N |
667.05 |
552.07 |
97.89 |
77.47 |
47.45 |
29.60 |
14.53 |
|
|
|
8 |
O |
871.41 |
739.29 |
138.12 |
113.9 |
77.41 |
54.94 |
35.12 |
13.62 |
|
|
9 |
F |
1103.12 |
953.91 |
185.19 |
157.17 |
114.24 |
87.14 |
62.71 |
34.97 |
17.42 |
|
10 |
Ne |
1362.2 |
1195.83 |
239.1 |
207.28 |
157.93 |
126.21 |
97.12 |
63.45 |
40.96 |
21.56 |
As we know, for the hydrogen atom, when it is in the resonance ionization process, their ionization energy is given as:
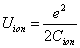
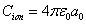
In generation, for the Z element, K electron, let us assume that their effective nuclear charge is:
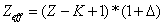
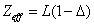
Where
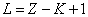
For K=1, the Z element first electron,
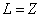
For K=Z, the Z element last electron,
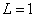
Thus we can get Z element, K electron ionization energy as:
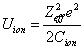
Where
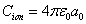
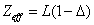
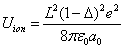
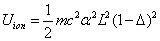
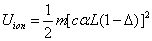
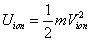
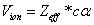
Within the Ionization process, the electron electromagnetic energy converted into kinetic energy, electrons escape from the nucleus, the escape speed is proportional to the effective charge of the nuclei.
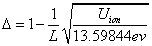
value table
|
1s1 |
1s2 |
2s1 |
2s2 |
2p1 |
2p2 |
2p3 |
2p4 |
2p5 |
2p6 |
||
Z |
K |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
H |
0 |
|
|
|
|
|
|
|
|
|
|
2 |
He |
0 |
-0.35 |
|
|
|
|
|
|
|
|
|
3 |
Li |
0 |
-0.18 |
0.37 |
|
|
|
|
|
|
|
|
4 |
Be |
0 |
-0.12 |
0.42 |
0.17 |
|
|
|
|
|
|
|
5 |
B |
0 |
-0.09 |
0.44 |
0.32 |
0.22 |
|
|
|
|
|
|
6 |
C |
0 |
-0.07 |
0.46 |
0.37 |
0.33 |
0.09 |
|
|
|
|
|
7 |
N |
0 |
-0.06 |
0.46 |
0.40 |
0.38 |
0.26 |
-0.03 |
|
|
|
|
8 |
O |
0 |
-0.05 |
0.47 |
0.42 |
0.40 |
0.33 |
0.2 |
0 |
|
|
|
9 |
F |
0 |
-0.05 |
0.47 |
0.43 |
0.42 |
0.37 |
0.28 |
0.2 |
-0.13 |
|
|
10 |
Ne |
0 |
-0.04 |
0.48 |
0.44 |
0.43 |
0.39 |
0.33 |
0.28 |
0.13 |
-0.26 |
|
Inside the hydrogen atom, we have
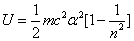
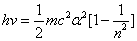
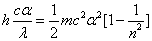
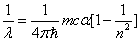
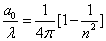
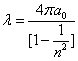
For the element Z, K electron, let us assume that the electron energy of the first spectra serial is as follows:
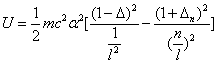
Where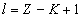
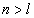
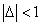
Then the electron energy of the j spectra serial is given as:
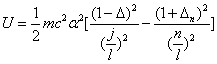
When
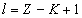
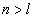
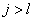
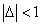
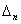Can be determined by a specific spectra line wavelength value
For the hydrogen atom, the first spectra serial
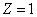
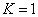
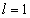
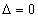
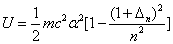
Hydrogen first spectra serial |
|||
n |
Intensity |
Wavelength(vacuum) |
|
2 |
500 |
1215.674 |
0.00079492 |
2 |
1000 |
1215.668 |
0.00078827 |
3 |
300 |
1025.722 |
0.00210893 |
4 |
100 |
972.5367 |
0.00395135 |
5 |
50 |
949.743 |
0.00631632 |
6 |
30 |
937.8034 |
0.00919858 |
7 |
20 |
930.7482 |
0.0125948 |
8 |
15 |
926.2256 |
0.0164982 |
For the helium atom, the first spectra serial of the first electron is given as
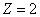
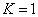
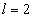
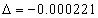
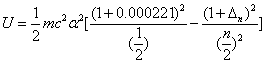
Helium first electron first spectra serial |
|||
n |
Intensity |
Wavelength(vacuum) |
|
2 |
500 P |
303.7858 |
0.001024 |
2 |
1000 P |
303.7804 |
0.000998 |
3 |
150 P |
256.3177 |
0.002337 |
3 |
300 P |
256.3166 |
0.00232 |
4 |
100 c |
243.0266 |
0.004169 |
5 |
50 c |
237.3307 |
0.006532 |
6 |
30 c |
234.3472 |
0.009417 |
7 |
20 c |
232.5842 |
0.012815 |
8 |
15 c |
231.4541 |
0.016725 |
For the helium atom, the second spectra serial of the first electron is given as
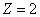
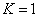
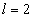
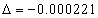
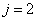
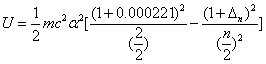
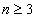
Helium first electron second spectra serial |
|||
n |
Intensity |
Wavelength(vacuum) |
|
3 |
15P |
1640.5326 |
0.000589808 |
3 |
25P |
1640.4897 |
0.000573476 |
3 |
180P |
1640.4742 |
0.000567574 |
3 |
25P |
1640.3914 |
0.000536048 |
3 |
7P |
1640.3750 |
0.000529803 |
3 |
50P |
1640.3447 |
0.000518265 |
3 |
120P |
1640.3321 |
0.000513467 |
4 |
50c |
1215.17 |
0.00105742 |
4 |
35 |
1215.09 |
0.00095877 |
5 |
30c |
1084.94 |
0.00160405 |
6 |
15c |
1025.27 |
0.00233436 |
7 |
8c |
992.36 |
0.00319109 |
8 |
6c |
972.11 |
0.00419641 |
9 |
5c |
958.70 |
0.00535842 |
For the helium atom, the first spectra serial of the second electron is as follows:
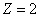
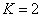
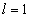
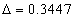
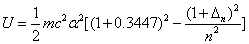
Helium second electron first spectra serial |
|||
n |
Intensity |
Wavelength(vacuum) |
|
2 |
50 |
591.4121 |
0.0341709 |
2 |
1000 |
584.3339 |
-0.0025752 |
3 |
400 |
537.0293 |
0.0010497 |
4 |
100 |
522.186 |
0.00485533 |
5 |
50 |
515.596 |
0.00999475 |
6 |
35 |
512.07 |
0.0152871 |
7 |
25 |
509.97 |
0.0217464 |
8 |
20 |
508.63 |
0.030658 |
9 |
15 |
507.71 |
0.0399277 |
10 |
10 |
507.08 |
0.0545745 |
11 |
7 |
506.56 |
0.0594603 |
12 |
5 |
506.31 |
0.0990477 |
13 |
4 |
505.90 |
0.0821738 |
14 |
3 |
505.75 |
0.119593 |
15 |
2 |
505.61 |
0.151823 |
For the Lithium atom, the first spectra serial of the first electron is written as
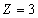
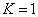
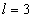
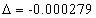
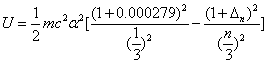
Lithium first electron first spectra serial |
|||
n |
Wavelength(vacuum) |
|
|
2 |
135.0011661 |
0.00109254 |
|
2 |
134.9957610 |
0.00103255 |
|
3 |
113.9057091 |
0.00239356 |
|
3 |
113.9045690 |
0.00235362 |
|
4 |
107.9992230 |
0.00422188 |
|
4 |
107.9987906 |
0.00419198 |
|
5 |
105.4679379 |
0.00657418 |
|
5 |
105.4677267 |
0.0065503 |
|
6 |
104.1420509 |
0.00944562 |
|
6 |
104.1419318 |
0.00942579 |
|
7 |
103.3585830 |
0.0128311 |
|
7 |
103.3585091 |
0.0128142 |
|
8 |
102.8563652 |
0.016725 |
|
8 |
102.8563162 |
0.0167103 |
|
For the Lithium atom, the first spectra serial of the second electron is as the following
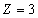
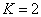
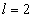
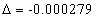
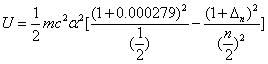
Lithium second electron first spectra serial |
|||
n |
Intensity |
Wavelength(vacuum) |
|
2 |
500 P |
303.7858 |
0.001024 |
2 |
1000 P |
303.7804 |
0.000998 |
3 |
150 P |
256.3177 |
0.002337 |
3 |
300 P |
256.3166 |
0.00232 |
4 |
100 c |
243.0266 |
0.004169 |
5 |
50 c |
237.3307 |
0.006532 |
6 |
30 c |
234.3472 |
0.009417 |
7 |
20 c |
232.5842 |
0.012815 |
8 |
15 c |
231.4541 |
0.016725 |
